Auto Queue Resizing & Adaptive Replica Selection
Table of Contents
| Author | Lee Hinman (lee@elastic.co) |
| Date | 2017-08-31 09:04:06 |
Introduction
There are no memes. Sorry.
This is a presentation about some of the recent work with Automatic Queue Resizing and Adaptive
Replica Selection (ARS).
In one of our all hands in Tahoe, we had a discussion topic about how we could change Elasticsearch to route around degraded or slower nodes. Both the queue resizing and adaptive replica selection are independent ways to tackle this issue. They address it in different ways though, and can be combined.
Of these features, the automatic queue resizing is available in Elasticsearch 6.0+ and adaptive
replicas selection will be available in Elasticsearch 6.1+ (assuming the PR is merged by then the
PR has been merged!).
Relevant Github issues and PRs
For the automatic queue resizing:
- https://github.com/elastic/elasticsearch/issues/3890
- https://github.com/elastic/elasticsearch/pull/23884
For adaptive replica selection:
Automatic Queue Resizing
In automatic queue resizing, we wanted a way where a node that was "degraded" to automatically
adjust its search threadpool queue_size to a lower value, thereby rejecting search queries that
are overloading the node.

Queue Resizing Implementation
The implementation is based on Little's Law, a simple formula
L = λW
Where L is the long term average number of requests, λ is the arrival rate of new requests, and
W is the average time a request spends being executed.
In Elasticsearch, there's a new threadpool type called fixed_auto_queue_size. To use it, the use
configures a target "response rate" they want the average response time be. So for instance, if a
user configures thread_pool.search.target_response_rate: 4s to a targeted response rate of four
seconds.
Now, assume the node is serving search requests at a rate of 15 reqs/s, so there can be 15 * 4 =
60 total requests in the queue at any particular time in order for . Elasticsearch can then adjust
the queue size towards this limit. If requests start to be served at a faster rate (the node is
recovering) then the queue can be increased, or if the node cannot serve them at 15 requests a
second, the queue can be lowered more. The minimum and maximum queue size can also be configured.
In Elasticsearch 6.0 the minimum and maximum are both configured to the initial size of 1000.
By default Elasticsearch can adjust the thread pool every thread_pool.search.auto_queue_frame_size
tasks, which defaults to 2000.
The Measured Impact
With a single node stressed1 in a 5-node cluster, this is the measured impact for average response time in milliseconds.
| No adjustment | Auto adjustment | % Change | |
|---|---|---|---|
| Test 1 | 8257.8 | 7181.2 | -13.037371 |
| Test 2 | 8257.8 | 6494.6 | -21.351934 |
This in particular helps with a particular customer who had a cluster where one node would constantly be "hot" due to unevenly distributed data, or degraded hardware. In addition, rather than having a node keel over due to being inundated with requests, a node can start rejecting them earlier.
Adaptive Replica Selection
Adaptive Replica Selection is an implementation of an academic paper called C3: Cutting Tail Latency in Cloud Data Stores via Adaptive Replica Selection
Originally, the paper was written for Cassandra, which means we had to adapt some things to fit Elasticsearch due to different behavior.
It's basically a formula where you "rank" each copy of the data to determine which is likeliest to be the "best" copy to send the request to. Instead of sending requests in a round-robin fashion to each copy of the data, ES can select the "best" version and route the request there.
This feature is turned off by default, but can be turned on dynamically by setting
cluster.routing.use_adaptive_replica_selection to true.
Adaptive Selection Implementation
The ARS formula is a little more complicated:
Ψ(s) = R(s) - 1/µ̄(s) + (q̂(s))^b / µ̄(s) Where q̂(s) is: q̂(s) = 1 + (os(s) * n) + q(s)
os(s)is the number of outstanding search requests to a nodenis the number of clients (data nodes) in the systemR(s)is the EWMA2 of the response time (as seen from the coordinating node) in millisecondsq(s)is the EWMA of the number of events in the thread pool queueµ̄(s)is the EWMA of service time of search events on the data node in milliseconds
For the moving averages, we use an α of 0.3 and for the formula we use a b value of 3 as
recommended in the C3 paper.
This was implemented in multiple PRs since it was a little more invasive, what happens is that basically with every query, we piggy-back information back to the coordinating node about the current queue size and EWMA service time for tasks.
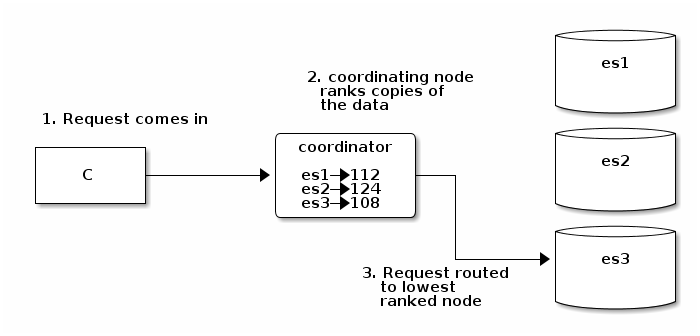
Assume you perform a query for an index that has data distributed on three different nodes. Elasticsearch scatters the query out to the data nodes. In this case, because we don't have any ranking information, all nodes are considered equal and we fall back to the regular round-robin of requests.
And along with the results, each node will return its current queue size and EWMA service time:
In addition, the coordinating node measures search requests for the EWMA of the response time of each node, keeping track of it locally. These numbers are then used for the next request, ranking each copy of the data to determine the best place to send the request. For instance, for three copies of the data on nodes with scores of 128, 108, and 113 respectively, the shard copy on node "data2" is chosen to serve the request.
After the routing is determined, the adaptive replica selection also adjusts the non-winning nodes' stats to gradually bring them towards the winning node's stats3. In doing this, we prevent a situation where a long GC that temporarily drastically increases a node's score causes the node not to receive any more requests ever.
The Measured Impact
This was tested with three "main" scenarios, a non-loaded and loaded setup with a client node handling all coordination, and a non-loaded cluster with requests sent in a round-robin manner.
Single replica, non-loaded case:
| Metric | No ARS | ARS | Change % |
|---|---|---|---|
| Median Throughput (ops/s) | 95.7866 | 98.537 | 2.8713828 |
| 50th percentile latency (ms) | 1003.29 | 970.15 | -3.3031327 |
| 90th percentile latency (ms) | 1339.69 | 1326.79 | -0.96290933 |
| 99th percentile latency (ms) | 1648.34 | 1648.8 | 0.027906864 |
So again, not a huge latency difference, as expected for the unloaded cluster.
Single replica, es3 under load:
| Metric | No ARS | ARS | Change % |
|---|---|---|---|
| Median throughput (ops/s) | 41.1558 | 87.8231 | 113.39179 |
| 50th percentile latency (ms) | 411.721 | 1007.22 | 144.63654 |
| 90th percentile latency (ms) | 5215.34 | 1839.46 | -64.729816 |
| 99th percentile latency (ms) | 6181.48 | 2433.55 | -60.631596 |
A large improvement in throughput for the loaded case as well as a trade-off of 50th percentile latency for a large improvement in 90th and 99th percentile latency. When a node is loaded we were able to route around the degraded node quite well.
Single replica, round robin requests:
| Metric | No ARS | ARS | Change % |
|---|---|---|---|
| Median throughput (ops/s) | 89.6289 | 95.9452 | 7.0471689 |
| 50th percentile latency (ms) | 1088.81 | 1013.61 | -6.9066228 |
| 90th percentile latency (ms) | 1706.07 | 1423.83 | -16.543284 |
| 99th percentile latency (ms) | 2481.1 | 1783.73 | -28.107291 |
Again a nice improvement in both throughput and latency for the non-stressed round-robin test case. So even if the cluster is experiencing even load, it can still help with throughput and latency.
Future Work
There's probably still work we can do to make this better. Part of the reason these are not on by default is that while they have shown good improvements in tests, and we tried to simulate user environments as well as we could, there's no way to know how they will impact every use case.
With automatic queue resizing, we require a human to know what the target_response_rate should be
for searches. It'd be nice if we didn't have to have this step.
Additionally, in particular with ARS, there are a number of values that are "tweakable" that we
don't currently expose, such as the α for the EWMA and b value for the queue adjustment.
Currently I don't think we want these to be exposed at all, as it's way too much complexity.
Footnotes:
stress -i 8 -c 8 -m 8 -d 8